Linear Regression:
It's a hypothetical model of the relationship between two variables.Here the model is linear
The two variables involved in this are called the Predictor(independent) and the response(dependent)
variable.
- Assumptions of Regression:
- Correlation:
It is used to assert the relationship between the variables, it could be strong/weak and positive/negative correlation.So we can describe the relationship with a straight line
- Differential effect:
This test involves ANOVA and T-test, they are used to show the effect among different groups in the variable.
- Normally distributed response variable.
Fit of the model: We use fitness of a model to show how good a model is in associating the variables.
-
Two factors are taken into considerations for this they are:
- Total Sum of Squares(SS T ):It is the sum of the squares of the difference of each data point from the mean of the outcome variable.
- Residual Sum of squares(SS R): It is the distance between each data point and the regression line
- SSM Difference between the two is the amount of variation accounted for by the model. This gives the Model variability.
- Residuals:It is the distance between the predicted value and the observed value.
Analysing the Regression Model:
R 2:
The R2 is the proportion of variance in the outcome (response) variable
which can be explained by the predictor (independent) variables. This gives the
usefulness of the model.
An R2 of 1 means the independent variable explains 100% of the variance in the
dependent variable. Conversely 0 means it explains none.
R 2 vs Adjusted R 2
- Every time we add a predictor to a model, the R-squared increases, even if due to chance alone. It never decreases. Therefore, a model with more terms may appear to have a better fit simply because it has more terms.
- If a model has too many predictors it begins to model the random noise in the data. This condition is known as overfitting the model and it produces misleadingly high R-squared values and a lessened ability to make predictions. Adjusted R2
- Adjusts value of R2 based on number of variables in the model. Adjusted R2 is reported for multiple linear regression
Analysis of Variance(ANOVA):
It shows whether the regression model is better at predicting the response variable than using the mean.
Beta Values:
It gives the unit change of the response value with respect to the predictor value.
Standardized Beta Values:Gives the value in terms of standard deviation.Useful
in case of comparing models.
Linear Regression equation:
Equation: y= b 0+ b 1X
where, b 0 is the intercept and b 1 is the regression coefficent.Coefficients:
Coefficients gives the values to construct the linear equation(i.e. The intecept and the regression coefficent)
Standardized Coefficients:These are used to find the standardised scores of the coefficients, which can be used to compare different models.
Multiple Linear Regression:
The relationship is described using a variation of the equation of a straight line.
Equation: y= b 0+ b 1X 1+b 2X 2+b 3X 3
where, b1 to bn are the regression coefficient for variable 1 to nDummy Variables:
Categorical variables are hard to predict because they do not have any scale and it would be impossible to associate
the change of it like a continous variable.
So we transform the categorical variable into a series of dummy variables which indicate whether a particular case
has that particular characteristic. They are also called as indicator variables.
- 0 (reference category) and 1 (category of interest)
- We can explore the differential effect for the category of interest when compared to the reference category
- For 'p' different categories there should be (p-1) indicator variables.
- Model 1:Comparing the relationship between mG2 and mG3:
Code:
#Model1 scatter <- ggplot(s_perform, aes(s_perform$mG2, s_perform$mG3)) #Add a regression line scatter + geom_point() + geom_smooth(method = "lm", colour = "Red", se = F) + labs(x = "mG2", y = "mG3") #Pearson Correlation stats::cor.test(s_perform$mG2, s_perform$mG3, method='pearson') #Building linear model using mG1,mG2 as predictors and mG3 as the dependent variable s_perform$mG3<-na_if(s_perform$mG3,0) model1<-lm(s_perform$mG3~s_perform$mG2) anova(model1) summary(model1) lm.beta::lm.beta(model1) stargazer(model1, type="text") #Tidy output of all the required statsResult:- The p-value indicates our model is significant, so we can reject the null hypothesis and accept the alternate hypothesis(We can predict the values of mG3 with predictor variable mG2)
- Increase marks in mG2 appears to associated with increase marks in mG3
- There appears to be a strong positvie correlation bewteen the two
- Therefore there is good justification for using regression to look at prediction.
- The F statistic looks at whether the model as whole is statistically significant
- In our case r 2 value is 0.9348, which means around 93.5% of the variance mG3 can be explained by mG2.
- Our linear regression model is Predicted mG3 = 0.32 + 0.99 * 'mG2'
- In our case using the standardised coefficents our model equation becomes: Predicted mG3 = 0 + 0.97 * 'mG2'
Output:> anova(model1) Analysis of Variance Table Response: s_perform$mG3 Df Sum Sq Mean Sq F value Pr(>F) s_perform$mG2 1 3444.5 3444.5 4902.1 < 2.2e-16 *** Residuals 341 239.6 0.7 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 > summary(model1) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2) Residuals: Min 1Q Median 3Q Max -2.2447 -0.2199 -0.1579 0.7925 2.7801 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.31921 0.16692 1.912 0.0567 . s_perform$mG2 0.98759 0.01411 70.015 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8382 on 341 degrees of freedom (39 observations deleted due to missingness) Multiple R-squared: 0.935, Adjusted R-squared: 0.9348 F-statistic: 4902 on 1 and 341 DF, p-value: < 2.2e-16 > lm.beta::lm.beta(model1) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2) Standardized Coefficients:: (Intercept) s_perform$mG2 0.0000000 0.9669345 > stargazer(model1, type="text") #Tidy output of all the required stats =============================================== Dependent variable: --------------------------- mG3 ----------------------------------------------- mG2 0.988*** (0.014) Constant 0.319* (0.167) ----------------------------------------------- Observations 343 R2 0.935 Adjusted R2 0.935 Residual Std. Error 0.838 (df = 341) F Statistic 4,902.121*** (df = 1; 341) =============================================== Note: *p< 0.1; **p< 0.05; ***p< 0.01
Checking Assumptions:- Outliers:
cooksd<-sort(cooks.distance(model1)) # plot Cook's distance plot(cooksd, pch="*", cex=2, main="Influential Obs by Cooks distance") abline(h = 4*mean(cooksd, na.rm=T), col="red") # add cutoff line text(x=1:length(cooksd)+1, y=cooksd, labels=ifelse(cooksd>4*mean(cooksd, na.rm=T),names(cooksd),""), col="red") # add labels #finding rows related to influential observations influential <- as.numeric(names(cooksd)[(cooksd > 4*mean(cooksd, na.rm=T))]) # influential row numbers influential stem(influential) head(s_perform[influential, ]) # influential observations. head(s_perform[influential, ]$mG1) # influential observations - look at the values of mG1 head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 car::outlierTest(model1) # Bonferonni p-value for most extreme obs - Are there any cases where the outcome variable has an unusual variable for its predictor values? - Leverage:
car::leveragePlots(model1) # leverage plots - Homocedasticity:
#Assess homocedasticity plot(model1,1) plot(model1, 3) - Residuals:
#Create histogram and density plot of the residuals plot(density(resid(model1))) #Create a QQ plotqqPlot(model, main="QQ Plot") #qq plot for studentized resid car::qqPlot(model1, main="QQ Plot") #qq plot for studentized resid
Output:> influential [1] 246 56 2 35 145 287 288 351 170 105 34 216 334 252 48 185 129 > stem(influential) The decimal point is 2 digit(s) to the right of the | 0 | 03456 1 | 13579 2 | 25599 3 | 35 > head(s_perform[influential, ]) # influential observations. # A tibble: 6 x 57 school sex age address famsize Pstatus Medu Fedu Mjob Fjob reason nursery internet guardian.m traveltime.m
1 GP M 16 U GT3 T 4 3 heal… serv… reput… yes yes mother 1 2 GP F 16 U GT3 T 2 2 serv… other reput… no yes mother 2 3 GP F 15 R GT3 T 1 1 other other reput… no yes mother 1 4 GP F 15 U LE3 T 1 1 at_h… other other yes yes mother 1 5 GP F 18 R GT3 T 1 1 at_h… other course no no mother 3 6 GP M 17 U GT3 T 2 1 other other home yes yes mother 2 # … with 42 more variables: studytime.m , failures.m , schoolsup.m , famsup.m , paid.m , # activities.m , higher.m , romantic.m , famrel.m , freetime.m , goout.m , Dalc.m , # Walc.m , health.m , absences.m , mG1 , mG2 , mG3 , guardian.p , traveltime.p , # studytime.p , failures.p , schoolsup.p , famsup.p , paid.p , activities.p , # higher.p , romantic.p , famrel.p , freetime.p , goout.p , Dalc.p , Walc.p , # health.p , absences.p , pG1 , pG2 , pG3 , intmark , Sex_num , inthighmG2 , # inthigher.m > head(s_perform[influential, ]$mG1) # influential observations - look at the values of mG1 [1] 19 13 8 7 9 8 > head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 [1] 20 11 5 10 10 10 > car::outlierTest(model1) # Bonferonni p-value for most extreme obs - Are there any cases where the outcome variable has an unusual variable for its predictor values? No Studentized residuals with Bonferroni p < 0.05 Largest |rstudent|: rstudent unadjusted p-value Bonferroni p 48 3.377184 0.00081718 0.28029 > car::qqPlot(model1, main="QQ Plot") #qq plot for studentized resid [1] 48 185 Plots: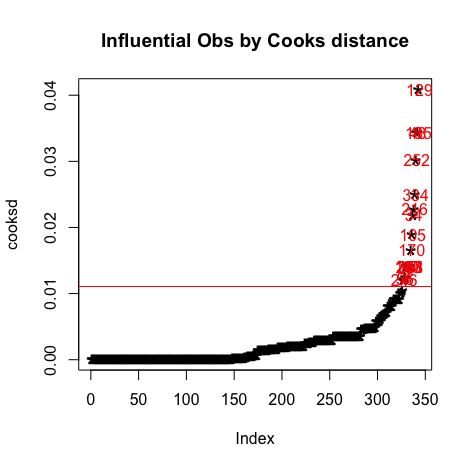
It can be observed that all the points are less than 1, So we don't have to worry about the outliers
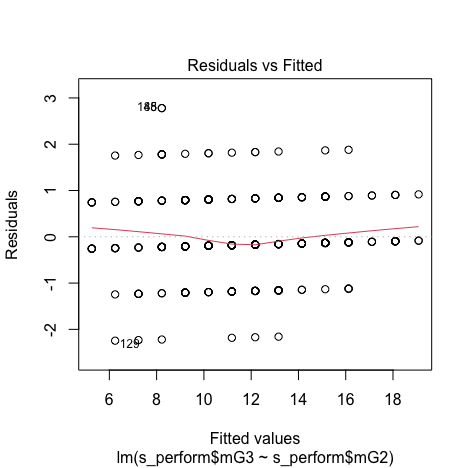
We can see that there is no pattern and points are equally distributed, therefore homoscedasticity is not an concern
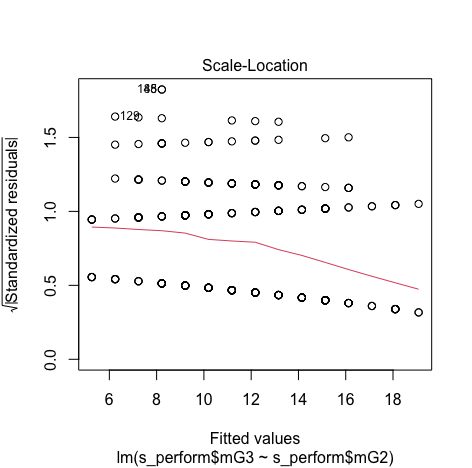
Minimum and Maximum value is within the acceptable range(-3.29,+3.29) hence we do not have outliers.
Though the red lines are slightly distorted but this is not a huge problem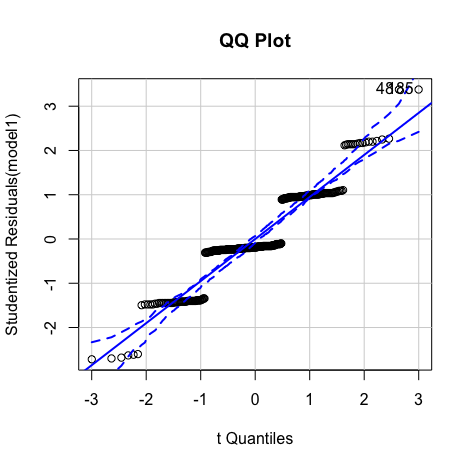
Errors are normally distributed
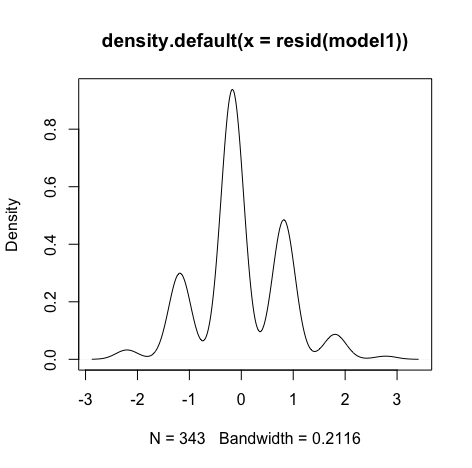
Errors are normally distributed
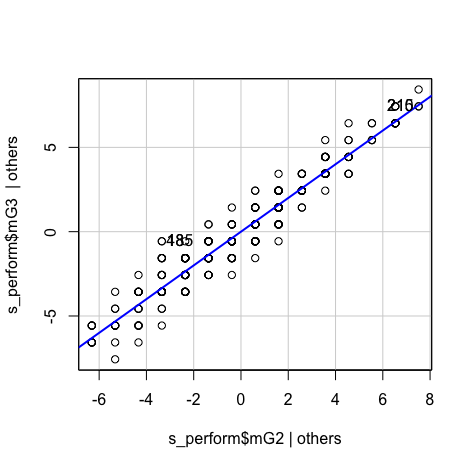
- Model 2:Multiple Linear Regression(with mG2 and Higher as predictors and mG3 as dependent
- We use the variable higher as a predictor, since it is a categorical type we use it as a dummy variable to understand the differential effect of the marks of students who are planning for higher studies and others.
- Here, 0 (reference category, no) and 1 (category of interest, yes)
Code:#Model2 model2<-lm(s_perform$mG3~s_perform$mG2+s_perform$higher.m) anova(model2) summary(model2) stargazer(model2, type="text") #Tidy output of all the required stats lm.beta(model2) stargazer(model1, model2, type="text")Result:- The p-value indicates our model is significant, so we can reject the null hypothesis and accept the alternate hypothesis(We can predict the values of mG3 with predictor variable mG2 and higher.m)
- From the F-statistics and the p-value, our model is still significant.
- New regression equation with higher.m as another predictor is: Predicted mG3 = 0.459 + 0.989 * 'mG2' - 0.161 * 'yes'
- The new standardised reqression equation is: Predicted mG3 = 0 + 0.968 * 'mG2' - 0.009* 'yes'
- when we calculate the equation for yes and no for higher studies:
yes mG3 = 0+0.968-0.009=0.959
no mG3=0+0.968=0.968 - We can see a small difference between the group yes and no.
- We can see a slight change in the coefficent compared to model 1.
- In this case the Adjusted R 2 is 0.9347 which mean it could explain 93.5% of the variance of the mG3 from mG2.
Output:> anova(model2) Analysis of Variance Table Response: s_perform$mG3 Df Sum Sq Mean Sq F value Pr(>F) s_perform$mG2 1 3444.5 3444.5 4893.2132 < 2e-16 *** s_perform$higher.m 1 0.3 0.3 0.3804 0.5378 Residuals 340 239.3 0.7 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 > summary(model2) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2 + s_perform$higher.m) Residuals: Min 1Q Median 3Q Max -2.2322 -0.2101 -0.1549 0.8009 2.7899 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.45893 0.28148 1.630 0.104 s_perform$mG2 0.98897 0.01429 69.189 < 2e-16 *** s_perform$higher.myes -0.16055 0.26033 -0.617 0.538 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.839 on 340 degrees of freedom (39 observations deleted due to missingness) Multiple R-squared: 0.935, Adjusted R-squared: 0.9347 F-statistic: 2447 on 2 and 340 DF, p-value: < 2.2e-16 > stargazer(model2, type="text") #Tidy output of all the required stats =============================================== Dependent variable: --------------------------- mG3 ----------------------------------------------- mG2 0.989*** (0.014) higher.myes -0.161 (0.260) Constant 0.459 (0.281) ----------------------------------------------- Observations 343 R2 0.935 Adjusted R2 0.935 Residual Std. Error 0.839 (df = 340) F Statistic 2,446.797*** (df = 2; 340) =============================================== Note: *p< 0.1; **p< 0.05; ***p< 0.01 > lm.beta(model2) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2 + s_perform$higher.m) Standardized Coefficients:: (Intercept) s_perform$mG2 s_perform$higher.myes 0.00000000 0.96828309 -0.00863115Comparing Model 1 and Model 2:> stargazer(model1, model2, type="text") ========================================================================= Dependent variable: ----------------------------------------------------- mG3 (1) (2) ------------------------------------------------------------------------- mG2 0.988*** 0.989*** (0.014) (0.014) higher.myes -0.161 (0.260) Constant 0.319* 0.459 (0.167) (0.281) ------------------------------------------------------------------------- Observations 343 343 R2 0.935 0.935 Adjusted R2 0.935 0.935 Residual Std. Error 0.838 (df = 341) 0.839 (df = 340) F Statistic 4,902.121*** (df = 1; 341) 2,446.797*** (df = 2; 340) ========================================================================= Note: *p< 0.1; **p< 0.05; ***p< 0.01- Both the models are significant.
- Adding the "higher" variable decreased the F-statistic of the model
Checking Assumptions:- Outliers:
#Influential Outliers - Cook's distance cooksd<-sort(cooks.distance(model2)) # plot Cook's distance plot(cooksd, pch="*", cex=2, main="Influential Obs by Cooks distance") abline(h = 4*mean(cooksd, na.rm=T), col="red") # add cutoff line text(x=1:length(cooksd)+1, y=cooksd, labels=ifelse(cooksd>4*mean(cooksd, na.rm=T),names(cooksd),""), col="red") # add labels #find rows related to influential observations influential <- as.numeric(names(cooksd)[(cooksd > 4*mean(cooksd, na.rm=T))]) # influential row numbers stem(influential) head(s_perform[influential, ]) # influential observations. head(s_perform[influential, ]$mG2) # influential observations - look at the values of mG2 head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 head(s_perform[influential, ]$higher.m) # influential observations -look at the values of higher car::outlierTest(model2) # Bonferonni p-value for most extreme obs - Are there any cases where the outcome variable has an unusual variable for its predictor values? - Leverage:
car::leveragePlots(model2) # leverage plots - Homocedasticity:
#Assess homocedasticity plot(model2,1) plot(model2, 3) - Residuals:
#Create histogram and density plot of the residuals plot(density(resid(model2))) #Create a QQ plotqqPlot(model, main="QQ Plot") #qq plot for studentized resid car::qqPlot(model2, main="QQ Plot") #qq plot for studentized resid - Collinearity:
#Collinearity vifmodel<-car::vif(model2) vifmodel #Tolerance 1/vifmodel
Output:> head(s_perform[influential, ]) # influential observations. # A tibble: 6 x 57 school sex age address famsize Pstatus Medu Fedu Mjob Fjob reason nursery internet guardian.m traveltime.m1 GP M 15 U LE3 T 4 3 teac… serv… home yes yes mother 1 2 GP F 15 U LE3 A 4 3 other other course yes yes mother 1 3 GP M 18 U LE3 T 3 3 serv… heal… home yes yes father 1 4 MS M 18 U LE3 T 1 3 at_h… serv… course yes yes mother 1 5 GP F 19 U GT3 T 0 1 at_h… other course no no other 1 6 GP M 16 U GT3 T 4 4 serv… serv… other yes yes mother 1 # … with 42 more variables: studytime.m , failures.m , schoolsup.m , famsup.m , paid.m , # activities.m , higher.m , romantic.m , famrel.m , freetime.m , goout.m , Dalc.m , # Walc.m , health.m , absences.m , mG1 , mG2 , mG3 , guardian.p , traveltime.p , # studytime.p , failures.p , schoolsup.p , famsup.p , paid.p , activities.p , # higher.p , romantic.p , famrel.p , freetime.p , goout.p , Dalc.p , Walc.p , # health.p , absences.p , pG1 , pG2 , pG3 , intmark , Sex_num , inthighmG2 , # inthigher.m > head(s_perform[influential, ]$mG2) # influential observations - look at the values of mG2 [1] 16 8 6 7 8 7 > head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 [1] 18 6 8 8 9 5 > head(s_perform[influential, ]$higher.m) # influential observations -look at the values of higher [1] "yes" "yes" "yes" "no" "no" "yes" > car::outlierTest(model2) # Bonferonni p-value for most extreme obs - Are there any cases where the outcome variable has an unusual variable for its predictor values? No Studentized residuals with Bonferroni p < 0.05 Largest |rstudent|: rstudent unadjusted p-value Bonferroni p 48 3.387117 0.00078934 0.27075 > car::leveragePlots(model2) # leverage plots > #A density plot of the residuals > plot(density(resid(model2))) > #Create a QQ plot qPlot(model, main="QQ Plot") #qq plot for studentized resid > car::qqPlot(model2, main="QQ Plot Model 2") #qq plot for studentized resid [1] 48 185 > #Collinearity > vifmodel<-car::vif(model2) > vifmodel s_perform$mG2 s_perform$higher.m 1.025022 1.025022 #Tolerance > 1/vifmodel s_perform$mG2 s_perform$higher.m 0.9755884 0.9755884 - We can observe that the VIF values are less than 2.5 and 1/VIF values are greater than 0.4 . So we do not have multicollinearity problem.
Plots: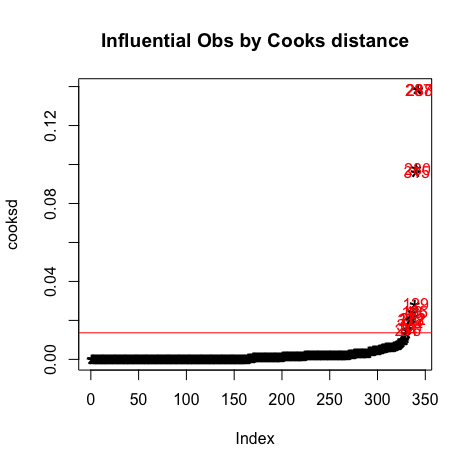
It can be observed that all the points are less than 1, So we don't have to worry about the outliers
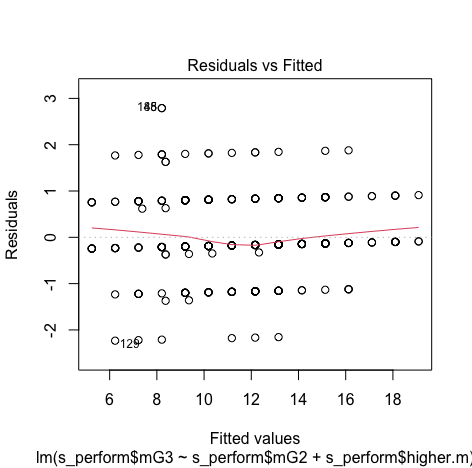
We can see that there is no pattern and points are equally distributed, therefore homoscedasticity is not an concern
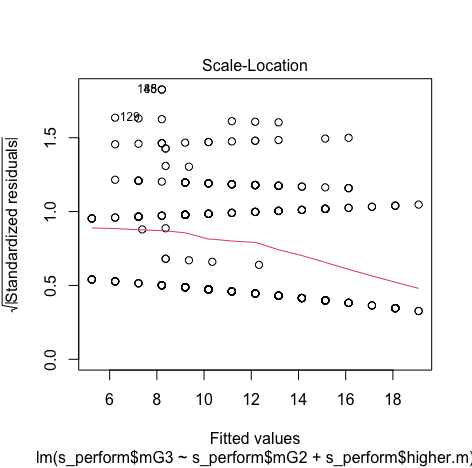
Minimum and Maximum value is within the acceptable range(-3.29,+3.29) hence we do not have outliers.
Though the red lines are slightly distorted but this is not a huge problem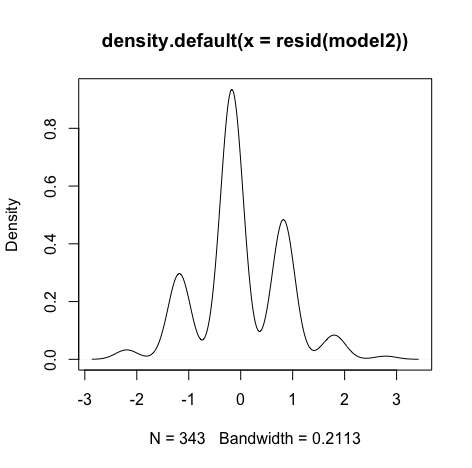
Errors are normally distributed
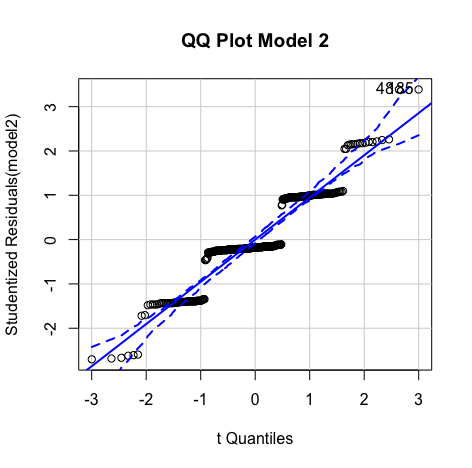
Errors are normally distributed
Reporting Multiple linear Regression(Model 2):
Multiple regression analysis was conducted to determine the student's final math grade(mG3).. Marks obtained in second grade(mG2),going for higher studies(higher) were used as predictor variables. In order to include the higher education in the regression model it was recorded dummy variable higher_edu (0 for no, 1 for yes).Examination of the histogram, normal P-P plot of standardised residuals and the scatterplot of the dependent variable, academic satisfaction, and standardised residuals showed that the some outliers existed. However, examination of the standardised residuals showed that none could be considered to have undue influence (95% within limits of -1.96 to plus 1.96 and none with Cook’s distance >1 as outlined in Field (2013). Examination for multicollinearity showed that the tolerance and variance influence factor measures were within acceptable levels (tolerance >0.4, VIF < 2.5 ) as outlined in Tarling (2008). The scatterplot of standardised residuals showed that the data met the assumptions of homogeneity of variance and linearity. The data also meets the assumption of non-zero variances of the predictors.
- Model 3:Multiple Linear Regression(with mG2 and Higher*mG2 as predictors and mG3 as dependent
variable.
- Model 2 was fine but it does assume that the gap in mG3 marks between students trying for higher studies and others remains constant (at 0.170 points) regardless of a student’s prior mG2 marks.
- But it may be that high achieving students who are not trying for higher studies at mG2 could be outperforming students who are trying for higher studies at mG3 and/or that low performing students trying for higher studies at mG2 may fall even further behind their students who are not trying for higher studies at mG3?
- We are hypothesising here, in effect, that the gradients of both these lines of best fit might not be the same and thus these two lines might not actually be parallel.
- We can test this hypothesis by adding what is referred to as an ‘interaction term’ to the model that is basically a new variable calculated by multiplying Higher’ by ‘mG2’.
Code:#Model 3 #interaction effect #create interaction term - adding a new variable to the dataset inthighmG2 s_perform$inthigher.m <- ifelse(s_perform$higher.m=='yes',1,0) s_perform$inthigher.m s_perform$inthighmG2<-as.numeric(s_perform$inthigher.m)*s_perform$mG2 s_perform$inthighmG2 model3 <-lm(s_perform$mG3~s_perform$mG2+s_perform$higher.m+s_perform$inthighmG2) anova(model3) summary(model3) stargazer(model3, type="text") #Tidy output of all the required stats lm.beta(model3) stargazer(model2, model3, type="text")Result:- The p-value indicates our model is significant, so we can reject the null hypothesis and accept the alternate hypothesis(We can predict the values of mG3 with predictor variable mG2, higher.m and indication term mG2*higher.m)
- From the F-statistics and the p-value, our model is still significant.
- New regression equation with higher.m as another predictor is: Predicted mG3 = 2.48 + 0.755 * 'mG2' -2.197 * 'yes' + 0.235 * 'yes*mG2'
- The new standardised reqression equation is: Predicted mG3 = 0+ 0.739 * 'mG2' -0.118 * 'yes'+ 0.269 * 'yes*mG2'
- when we calculate the equation for yes and no for higher studies with the interaction:
yes mG3 = 0+0.739-0.118+0.269=0.89
no mG3=0+0.739+0.269=1.008 - We can see how the inclusion of the interaction term has basically had the consequence of giving us two lines of best fit (one for yes and one for no) that now have differing intercepts as well as differing gradients or slopes.
- On this occasion we already knew that the difference in the slopes was minor (and not statistically significant) and this is confirmed by these two lines of best fit where the difference in the gradients of both lines (0.739 compared to 0.968) is marginal and wouldn’t even be obvious to the eye if the two lines were plotted on a graph.
- We would conclude that this interaction term has no significant effect on the model.
- In this case the Adjusted R 2 is 0.9347 which mean it could explain 93.5% of the variance of the mG3 from mG2.
Output:> anova(model3) Analysis of Variance Table Response: s_perform$mG3 Df Sum Sq Mean Sq F value Pr(>F) s_perform$mG2 1 3444.5 3444.5 4899.7341 < 2e-16 *** s_perform$higher.m 1 0.3 0.3 0.3809 0.5375 s_perform$inthighmG2 1 1.0 1.0 1.4531 0.2289 Residuals 339 238.3 0.7 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 > summary(model3) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2 + s_perform$higher.m + s_perform$inthighmG2) Residuals: Min 1Q Median 3Q Max -2.2252 -0.2057 -0.1569 0.8041 2.7943 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 2.4804 1.7004 1.459 0.145565 s_perform$mG2 0.7549 0.1947 3.877 0.000127 *** s_perform$higher.myes -2.1966 1.7089 -1.285 0.199549 s_perform$inthighmG2 0.2353 0.1952 1.205 0.228872 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 0.8385 on 339 degrees of freedom (39 observations deleted due to missingness) Multiple R-squared: 0.9353, Adjusted R-squared: 0.9347 F-statistic: 1634 on 3 and 339 DF, p-value: < 2.2e-16 > stargazer(model3, type="text") #Tidy output of all the required stats =============================================== Dependent variable: --------------------------- mG3 ----------------------------------------------- mG2 0.755*** (0.195) higher.myes -2.197 (1.709) inthighmG2 0.235 (0.195) Constant 2.480 (1.700) ----------------------------------------------- Observations 343 R2 0.935 Adjusted R2 0.935 Residual Std. Error 0.838 (df = 339) F Statistic 1,633.856*** (df = 3; 339) =============================================== Note: *p< 0.1; **p< 0.05; ***p< 0.01 > lm.beta(model3) Call: lm(formula = s_perform$mG3 ~ s_perform$mG2 + s_perform$higher.m + s_perform$inthighmG2) Standardized Coefficients:: (Intercept) s_perform$mG2 s_perform$higher.myes s_perform$inthighmG2 0.0000000 0.7391138 -0.1180848 0.2694700Comparing Model 2 and Model 3:> stargazer(model2, model3, type="text") ========================================================================= Dependent variable: ----------------------------------------------------- mG3 (1) (2) ------------------------------------------------------------------------- mG2 0.989*** 0.755*** (0.014) (0.195) higher.myes -0.161 -2.197 (0.260) (1.709) inthighmG2 0.235 (0.195) Constant 0.459 2.480 (0.281) (1.700) ------------------------------------------------------------------------- Observations 343 343 R2 0.935 0.935 Adjusted R2 0.935 0.935 Residual Std. Error 0.839 (df = 340) 0.838 (df = 339) F Statistic 2,446.797*** (df = 2; 340) 1,633.856*** (df = 3; 339) ========================================================================= Note: *p< 0.1; **p< 0.05; ***p< 0.01- Both the models are significant.
- Adding the "higher" variable decreased the F-statistic of the model
Checking Assumptions:- Outliers:
#Influential Outliers - Cook's distance cooksd<-sort(cooks.distance(model3)) # plot Cook's distance plot(cooksd, pch="*", cex=2, main="Influential Obs by Cooks distance") abline(h = 4*mean(cooksd, na.rm=T), col="red") # add cutoff line text(x=1:length(cooksd)+1, y=cooksd, labels=ifelse(cooksd>4*mean(cooksd, na.rm=T),names(cooksd),""), col="red") # add labels #find rows related to influential observations influential <- as.numeric(names(cooksd)[(cooksd > 4*mean(cooksd, na.rm=T))]) # influential row numbers stem(influential) head(s_perform[influential, ]) # influential observations. head(s_perform[influential, ]$mG2) # influential observations - look at the values of mG2 head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 head(s_perform[influential, ]$higher.m) # influential observations -look at the values of higher head(s_perform[influential, ]$inthighmG2) # influential observations -look at the values of interaction var - Leverage:
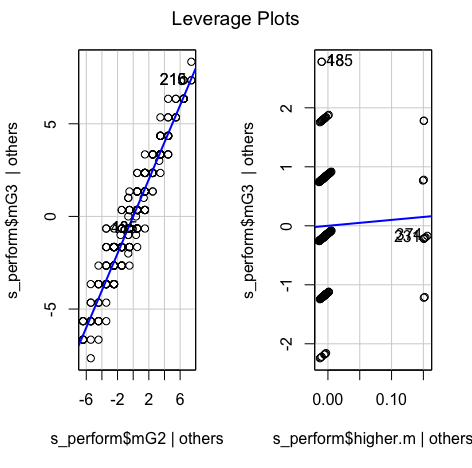
car::leveragePlots(model3) # leverage plots - Homocedasticity:
#Assess homocedasticity plot(model3,1) plot(model3, 3) - Residuals:
#Create histogram and density plot of the residuals plot(density(resid(model3))) #Create a QQ plotqqPlot(model, main="QQ Plot") #qq plot for studentized resid car::qqPlot(model1, main="QQ Plot") #qq plot for studentized resid - Collinearity:
#Collinearity vifmodel<-car::vif(model2) vifmodel #Tolerance 1/vifmodel
Results:> head(s_perform[influential, ]) # influential observations. # A tibble: 6 x 57 school sex age address famsize Pstatus Medu Fedu Mjob Fjob reason nursery internet guardian.m traveltime.m1 GP F 16 U GT3 T 1 1 serv… serv… course no yes father 4 2 GP M 15 U GT3 T 2 2 serv… serv… course yes yes father 1 3 GP F 17 U GT3 T 4 3 other other reput… yes yes mother 1 4 GP M 18 U GT3 T 2 1 serv… serv… other no yes mother 1 5 GP M 17 U GT3 T 2 1 other other home yes yes mother 2 6 GP M 17 U GT3 T 2 1 other other home yes yes mother 2 # … with 42 more variables: studytime.m , failures.m , schoolsup.m , famsup.m , paid.m , # activities.m , higher.m , romantic.m , famrel.m , freetime.m , goout.m , Dalc.m , # Walc.m , health.m , absences.m , mG1 , mG2 , mG3 , guardian.p , traveltime.p , # studytime.p , failures.p , schoolsup.p , famsup.p , paid.p , activities.p , # higher.p , romantic.p , famrel.p , freetime.p , goout.p , Dalc.p , Walc.p , # health.p , absences.p , pG1 , pG2 , pG3 , intmark , Sex_num , inthighmG2 , # inthigher.m > head(s_perform[influential, ]$mG2) # influential observations - look at the values of mG2 [1] 8 8 6 9 8 8 > head(s_perform[influential, ]$mG3) # influential observations - look at the values of mG3 [1] 11 11 4 8 10 10 > head(s_perform[influential, ]$higher.m) # influential observations -look at the values of higher [1] "yes" "yes" "yes" "no" "no" "no" > head(s_perform[influential, ]$inthighmG2) # influential observations -look at the values of interaction var [1] 8 8 6 0 0 0 > car::outlierTest(model3) # Bonferonni p-value for most extreme obs - Are there any cases where the outcome variable has an unusual variable for its predictor values? No Studentized residuals with Bonferroni p < 0.05 Largest |rstudent|: rstudent unadjusted p-value Bonferroni p 48 3.395179 0.00076746 0.26324 > car::leveragePlots(model3) # leverage plots > #Assess homocedasticity > plot(model3,1) > plot(model3, 3) > #A density plot of the residuals > plot(density(resid(model3))) > #Create a QQ plot qPlot(model, main="QQ Plot") #qq plot for studentized resid > car::qqPlot(model3, main="QQ Plot Model 3") #qq plot for studentized resid [1] 48 185 vifmodel s_perform$mG2 s_perform$higher.m s_perform$inthighmG2 190.43212 44.23102 261.88128 > #Tolerance > 1/vifmodel s_perform$mG2 s_perform$higher.m s_perform$inthighmG2 0.005251215 0.022608568 0.003818524 - We can observe that the VIF values are greater than 2.5 and 1/VIF values are less than 0.4 . So we have multicollinearity problem.
- After adding the interaction term we can observe multicollinearity in the model.
Plots: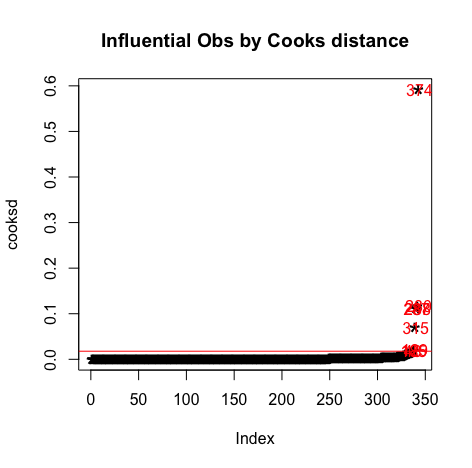
It can be observed that all the points are less than 1, So we don't have to worry about the outliers
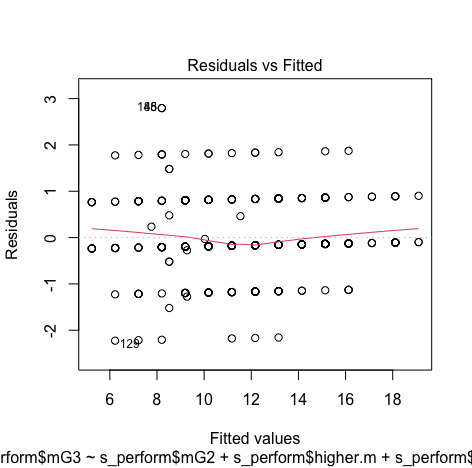
We can see that there is no pattern and points are equally distributed, therefore homoscedasticity is not an concern
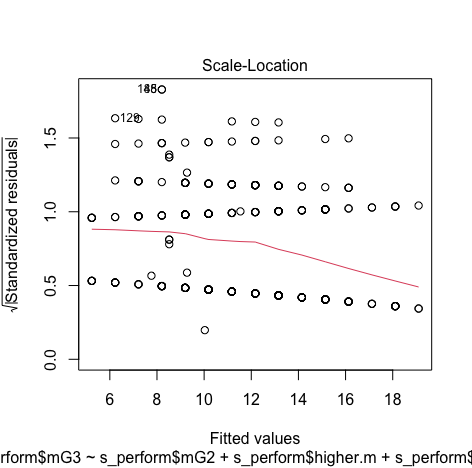
Minimum and Maximum value is within the acceptable range(-3.29,+3.29) hence we do not have outliers.
Though the red lines are slightly distorted but this is not a huge problem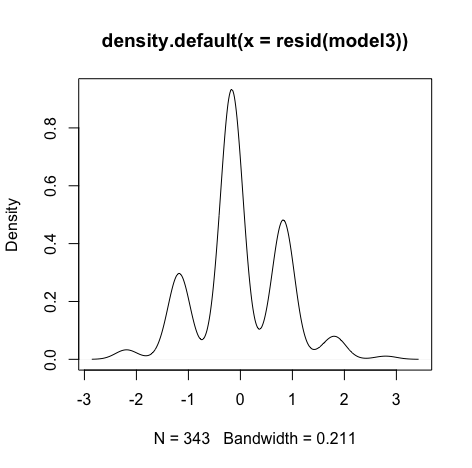
Errors are normally distributed
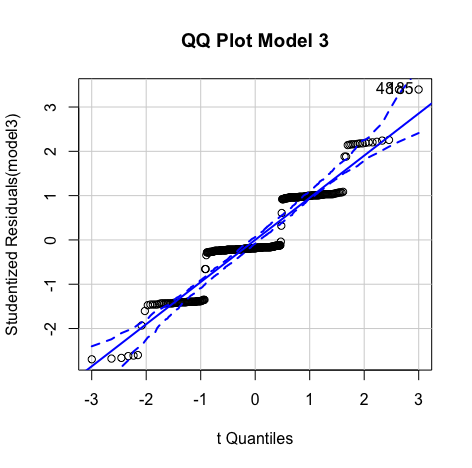
Errors are normally distributed
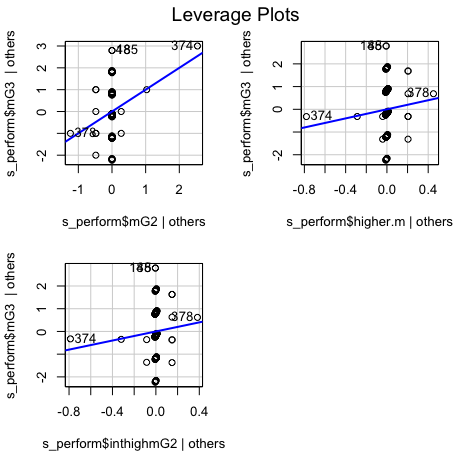
Research Question 5:
Can we predict mG3 value with various predictors using linear Regression ? Null Hypothesis: The values of mG3 cannot be predicted with the predictor variables(mG2, higher.m) using linear Regression. Alternate Hypothesis: The values of mG3 can be predicted with the predictor variables(mG2, higher.m) using linear Regression.Models:
Reporting Multiple linear Regression(Model 3):
Multiple regression analysis was conducted to determine the student's final math grade(mG3).. Marks obtained in second grade(mG2),going for higher studies(higher) were used as predictor variables In order to include the higher education in the regression model it was recorded dummy variable higher_edu (0 for no, 1 for yes) and an interaction term was introduced by multiplying (inthigher * mG2) .Examination of the histogram, normal P-P plot of standardised residuals and the scatterplot of the dependent variable, academic satisfaction, and standardised residuals showed that the some outliers existed. However, examination of the standardised residuals showed that none could be considered to have undue influence (95% within limits of -1.96 to plus 1.96 and none with Cook’s distance >1 as outlined in Field (2013). Examination for multicollinearity showed that the tolerance and variance influence factor measures were outside acceptable levels (tolerance < 0.4, VIF > 2.5 ) as outlined in Tarling (2008).